About Arcsec to Parsec

What is the actual size of that building that you see far away? The apparent size versus the actual size

What is the actual size of that building that you see far away? What about the Moon? How big in the sky will be the Sun if it were ten times farther? How big will be the Earth in the sky if it was orbiting our closest star?

These questions relate the apparent size of an object with its actual size.

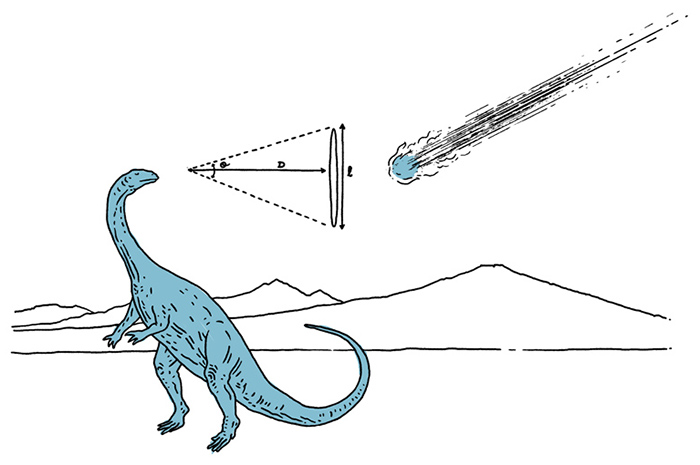
The apparent size is the angle of an object as seen from a given position, also know as angular diameter, angular size or visual angle. Units used to describe the apparent size of an object are for example, radians, degrees or arcminutes.

The actual size is the measured dimension of an object, also know as linear size. Units used to describe the linear size of an object are for example, meters, feet or kiloparsec.

The apparent size and the actual size of one object can be related if one knows the actual distance from the observer to the object.

So, why Arc2parc converter?

Arc2parc is a javascript calculator that converts the apparent size of an object to its linear size or viceversa providing the distance between the object and the observer. For objects close to the observer this is basically just a simple trigonometry problem (see below). However, for objects really far far away things get a little more complicated. The specific characterisc cosmological model in which we live affects the way light travel to us and therefore this relation. In this case the equation that relates these two parameters is not as simple or straightforwad and requires some more elaborated calculations (see below).

One relevant issue that has motivated this calculator is that observational astrophysics tend to speak in terms of angular size (degrees, arcminutes, etc) because this is much more useful when you are dealing with telescopes and planning observations. However theoretical astrophysicists tend to use the linear size (kiloparsec, meters, etc).

This calculator aims to be a simple tool to transform the linear size into angular size or viceversa to facilitate informal discussions in the astrophysical community during coffee breaks, arxiv sessions, workshops, etc.

Want to try it? What's the diameter of the Moon?

But this calculator has been built also just for you to play around. Do you want to start?

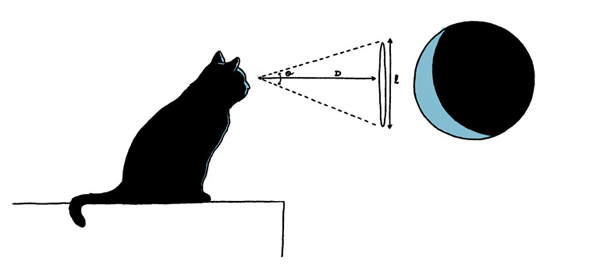
Try these numbers:

• The mean value of the distance between the Earth and the Moon is around 384400 kilometers.
• The Moon has a mean angular size in the night sky around 29.30 arcminutes.

What is the approximate diameter of the Moon?

Notice that the Moon is very close to us so you will need to change the calculator method to trigonometry (Options Section). You can check your answer here.

Notice also that the orbit of the Moon around the Earth is not circular, and therefore the distance between the two changes from the apogee (farthest point) and perigee (closest point) as well as its angular size. The difference between the two distances is around 11% level.

Understanding the math behind it

Now a bit more on the math behind this calculator. The relation between the actual size of an object, its angular size seen by an observer and the distance between the two can be obtained using some simple trigonometry relation. The above picture illustrates the relation between these three parameters.

$\tan \left(\frac{\theta}{2}\right)=\frac{l}{2D}$

where θ is the angular size, l is the linear size, and D is the distance. For more information on this subject you can start here.

However the trigonometry solution is not correct when we consider very big distances. Why?

General relativity tell us that we have to consider the cosmological model of our Universe (i.e. its shape and energy content) because it affects how the light travels to an observer.

Taking this into account we can relate the angular size, θ, and the linear size, l, of an object with the Angular distance, D_A(a):

$l= D_{\rm A}(a)\times \theta$

The angular distance (also known as angular diameter distance or angular size distance) of a far object depends on the assumed cosmology of the Universe and can be written as:

$D_{\rm A}(a)=\left\{ \begin{array}{ll} \frac{ac}{H_{o}\sqrt{-\Omega_{K}}} \sin[\frac{H_{0}\sqrt{-\Omega_{K}}}{c}D_{\rm C}(a)] & \quad \text{if $\Omega_{K}<0$}\\\\ aD_{\rm C}(a) & \quad \text{if $\Omega_{K}=0$}\\\\ \frac{ac}{H_{o}\sqrt{\Omega_{K}}} \sinh[\frac{H_{0}\sqrt{\Omega_{K}}}{c}D_{\rm C}(a)] & \quad \text{if $\Omega_{K}>0$} \end{array} \right. $

where:

$D_{\rm C}(a)= c \int_{a}^{1} \frac{1}{a\dot{a}}da$

a is the scale factor and ȧ is:

$\dot{a}=H_{o}\sqrt{\frac{\Omega_{R}}{a^{2}}+\frac{\Omega_{M}}{a}+\Omega_{K}+\Omega_{\Lambda}a^{2}}$

with H₀ being the Hubble constant and Ω_R, Ω_M, Ω_K, Ω_L stand for the different energy density content of the Universe. As you see this relation is not as straightforward as for the trigonometry approach but do not worry, it is not as terrible as it looks specially thanks to computers. This calculator is doing all the math for you!

For more information on this subject you can start here. Also if you are just interested in the values of some different cosmological parameters related with these quantities you may find useful these cosmological calculators: UCLA Prof. Wright Cosmological Calculator, U.Wyoming Prof. Kobulnicky Cosmology Calculator, U. Chicago Prof. Gnedin Cosmological Calculator for the Flat Universe, Relativity-4-Engineers Cosmological Calculator.

The default distance used in this calculator is the metric radial distance or comoving distance between two points now, D_C(a). However sometimes the light travel time distance is used to describe how far is an object. This way of measuring distance tells us how much time took the light to travel from the object to the observer. This distance is not the same as the metric radial distance, specially for very far away objects. Althought this definition of distance can be misleading (read also UCLA Prof. Wright's opinion on this), it is widely use in science press realeases so we have also included this option in the calculator. You will usually see this distance in units of light Gigayears or light years but notice that only the units do not tell you which definition of distance has been used.

Finally, nowdays some areas of astrophysics need not only the accurate computation of these cosmological distances but also its calculation in an incredible big number (e.g. in lensing studies). To improve the speed of these calculations some authors have developed fitting formulas of the solutions valid for some specific cosmological models. The arc2parc calculator has also implemented some of these fit formulas: Pen 1999, Wickramasinghe et al. 2010 and Liu et al. 2011. We refer the reader to these papers for more details about them.

For any questions, comments and/or suggestions please do not hesitate to contact us.